Reinforcement Learning and Creative Applications

This month we had an introductory overview of Reinforcement Learning, currently a very active area of research this is behind some of the most impressive achievements for machine learning.

The speaker's slides are similar to the UCL course slides: [link].

A video recording of the talk, including questions and answers, is online: [link].

In this write-up, I won't repeat closely the content of the talk, but instead provide my own summary of the key points, and examples of simple but illustrative code that uses reinforcement learning to solve a maze problem.

Reinforcement Learning?

We were lucky to have Ali Choudhry, a PhD researcher in AI and Education, and advocate for reinforcement learning, lead this session and share his expertise.

It is a common perception that deep neural networks have been solely responsible for the huge leaps in artificial intelligence in recent years. In fact, reinforcement learning has been core to these headline grabbing advances, often in combination with neural networks.

A notable example is Google DeepMind's AlphaGo Zero which learned to play the 3,000 year old game of Go, which has simple rules but is immensely complex in its gameplay and strategy. In fact AlphaGo Zero learned new strategies thought not to have been discovered by human players during those 3000 years!

Google DeepMind's AlphaGo system used RL to learn strategies to beat
the world's leading Go player.

Ali explained that that current trends in academic research, conferences and industrial applications, reinforcement learning is on an upward trajectory, which some believe will surpass the already significant advances from neural network-based deep learning.

To help clarify the idea of reinforcement learning, Ali started by comparing it to supervised and unsupervised learning.

• Supervised Learning - when a machine learning model learns from examples of question-answer pairs. Neural networks are commonly trained with examples.

• Unsupervised Learning - where an algorithm tries to find patterns, for example clusters, within data.

Reinforcement Learning, or RL, is the training of an agent based on its interaction with an environment, guided by rewards when it manages to navigate a good path or to a desired target.

This means that the learning does depend on the path the agent takes, unlike the more data-based supervised and unsupervised learning.

That description, and many you'll find in textbooks and courses, is admittedly a little abstract, so let's illustrate RL with an example.

Simple Example In Plain English

Before diving into RL methods, let's develop an intuition for how they work without using the terminology or mathematical expressions.

Have a look at the following very simple maze. There is a robot which we need to train so that it travels to the reward.

Without thinking too much about the technicalities of reinforcement learning, or indeed any kind of machine learning, let's ask ourselves how we'd do if we were 10 years old.

We'd probably come up with a very simple idea of "closeness" to the reward. Remember those childhood games where someone was "getting warmer" if they were closer to a hidden reward? Let's apply that same idea of warmness.

Having a value, a number, for how hot or cold each location is makes intuitive sense. Whichever location the robot is in, it just needs to move the the next one which has a hotter value. If it does this, it will get to the reward.

That seems easy enough, and a concept everyone can understand.

The challenge is, when we start in a new unknown environment, the robot don't know what the hotness values for each location are.

This is what reinforcement learning does - it explores the environment, taking many different paths, and uses that experience, some of which is rewarded, to work out what the hotness map looks like.

That's a simplified definition but it will take us far at this stage of our learning.

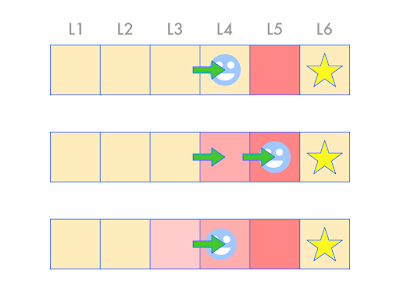
Have a look at the following picture showing the robot moving right, one cell at a time.

When it moves right one cell, from location L3 to L4, nothing has been learned. There is no reward, and no new information about whether we did a good or bad move.

When it moves right again to L5, again there is no new information, so nothing has been learned.

Finally when it moves right a third time to L6, the robot lands on the reward. This great! But what does it tell us?

It tells us that L5 is close to the target and should have a high "hotness" value. That's why we've coloured it a bright red.

Having coloured L5 a hot red, we look back and see that L4 is still not coloured with a hotness value. That's because, when we visited it, we didn't know it was a good place to be, that it was close to the reward.

One way to fix this is to remember our path from L3, and give all the cells on our path a hotness value, with L5 being the hottest, and L3 a lower value.

Instead of having to remember our journey, which could get very long in another scenario, we could save memory and just repeat the journeys.

Have a look at the next picture. It shows two more journeys, not just the progression of one journey.

On the second journey starting from L3, after the very fist one above, we reach L4 and can see that L5 is hot. We can use this information to give a slightly less hot value to L4. That's because being in L4 is good, but not as good as L5.

A third journey doesn't need to go anywhere because at the starting point L3 we can see that the next cell L4 is fairly hot. We can use this to colour our cell L3 with a mild hot value.

You can see how this process does create a "hotness / closeness" map.

It's now easy to see how this method can work with a more complex maze, trying different journeys to build up a map of hotness.

This very simplified example has the essence of reinforcement learning:

• we explore different journeys in our environment
• if we find a reward we mark the cell that got us there with a high score
• we repeat more journeys, and if we encounter cells with good scores, we can consider them as partial rewards, and mark the cells that got us to those with a slightly lower score

Having seen this example, we can now appreciate some of the things that set reinforcement learning apart:

• there is no labelled training data in the usual form (input data, output class)
• in fact, any information that we can use to learn from, might appear after many iterations of training, or not at all
• the training data is not independent of what the robot does, it depends on that path we take
• we don't use lots of memory to remember the paths we took, which can potentially be very long, we limit memory use to just the positions we've visited and the value of those positions

Before we move onto the next section, have a look at the next picture which shows how a maze with two routes is coloured.

If the robot follows the longer non-optimal path then we can see hotness values become colder the further back we are from the target. At the starting point, the robot sees that going right moves it to a warmer cell than the current one. Going upwards moves it to a much colder cell than the current one. So the robot should choose moving right,

This example shows two things relevant to RL:

• how a robot makes a choice between multiple options, choosing the path that gets hottest quickest
• how working back from the target leaves longer paths with colder cells

Some Terminology

The field of reinforcement learning has a fair bit of its own terminology and it helps to know the key terms.

The following links this new terminology to the robot example to help us understand it better:

• the robot is an agent, it is the agent that is doing the learning
• the maze is an environment, the agent interacts with the environment
• the information that describes where the robot is in the maze is called the state
• deciding what the agent does next is called a policy - with our robot, it was random movement or following the higher value cells
• what the agent does is called an action, and this results in a change of state
• the information we use to learn from is called a reward, and usually comes from a goal state
• the benefit of being in a state is called a value, and this is like the hotness number we used for each cell

Reinforcement Learning Worked Example

Let's use the simple robot example again, but this time, let's start to use numbers and do the calculations so we can see how they work.

The following picture shows the robot at state L3.

Because we have no information at all yet, we start with state values all set to zero.

If the robot looks to the right it sees L4 as having zero value. That is, there is no reward. So the value of L3 remains unchanged. If the robot looks to the left, to L2, it has zero value, so again, the value of L3 is unchanged.

If the robot moves to the right to L4, again we have no new information. Looking at L3 and L5 we see both are zero. So our L4 value remains zero.

So far, all the state values are zero:

If we then move right again to L5, things change. Looking left to L4 we see it has zero value. But if we look right at L6 we see that it's a target state and has a reward of 1.0.

Let's update the value of state L5:

$$
\begin{align}
V(s) & \leftarrow \underset{s'} {max} \left ( R(s') + \gamma \cdot V(s') \right ) \\
V(s) & \leftarrow 1.0 + 0.9 \cdot 0 \\
V(s) & \leftarrow 1.0  \\
\end{align}
$$

The $R(s')$ is the reward for getting to the next state $s'$. The $V(s')$ is the value of the state $s'$.

We've used a discount $\gamma = 0.9$, but it hasn't made a difference here because the value of L6 is 0, even though it is a target state.

Note that the equation asks us to use the next state $s'$ that maximises the update.

Let's look at the value of the states now.

Great - we can see that being in L5 is a good thing!

Let's run another journey.

If we start again in L3, looking to the left and right at L2 and L4 we see they have values of 0, so there are no useful updates.

Let's see the maths doing the right thing:

$$
\begin{align}
V(s) & \leftarrow \underset{s'} {max} \left ( R(s') + \gamma \cdot V(s') \right ) \\
V(s) & \leftarrow 0 + 0.9 \cdot 0 \\
V(s) & \leftarrow 0 \\
\end{align}
$$

Let's move to state L4.

This time we look right and see that L5 has a value, which it picked up from the previous journey. This means L4 will get a new value.

$$
\begin{align}
V(s) & \leftarrow \underset{s'} {max} \left ( R(s') + \gamma \cdot V(s') \right ) \\
V(s) & \leftarrow 0 + 0.9 \cdot 1.0 \\
V(s) & \leftarrow 0.9 \\
\end{align}
$$

So the value of L4 becomes 0.9, which 1.0 discounted by 0.9.

Here's the table of state values so far.

You can see how repeating the journeys will result in the table converging to the following:

This map of state values guides our robot towards the target.

You might be concerned that revisiting a state might change the value. If we look again at L4, we can see that the value from the left would be $0.9 * 0.81$, and from the right it would be $0.9 * 1$. Taking the maximum gives us 0.9 again.

Good States, Good Actions

What we've just done above is calculate how good each position in the maze is using actual numbers, and it mirrors what we did earlier with the intuitive example of hotness and coldness.

A more common approach in RL is to work out which actions are good, rather than focus on which states are good. That is, which moves are good rather than which locations.

The two are obviously related as actions are what take the agent from one state to another state.

The terminology uses what's called a Q-value for quality value, which takes into account both state and action.

Have a look at this picture which shows the agent one step away from the reward.

Whats the value of moving to the right? It's clearly a good move as it takes us to the target, which gives us a reward of 1.0. It makes sense that the value of moving right from L5 has the maximum value, we can call it 1.0.

What if the agent is in L4, two steps away from the reward?

We can use the same idea of using a discount for a future reward. If our discount is $\gamma = 0.9$, then the value of moving right from L4 is 0.9. We are assuming that the step after this one is optimal.

Let's now look at the value of a move in what looks like the wrong direction.

What's the value of a move left from L5?

If we follow our previous logic, it is the discounted value if we followed the optimal path. So the Q-value is 0.9 * the maximum Q-value out of L4 (which is moving right).

Let's write the general update rule:

$$
Q(s, a) \leftarrow \underset{a'} {max} \left ( R(s') + \gamma \cdot Q(s', a') \right )
$$

For the agent in L5, the value of moving right is, $Q(L5, right)$:

$$
\begin{align}
Q(L5, right) & \leftarrow \underset{a'} {max} \left ( R(s') + \gamma \cdot Q(s', a') \right ) \\
V(s) & \leftarrow 1.0 + 0.9 \cdot 0 \\
V(s) & \leftarrow 1.0 \\
\end{align}
$$

So $Q(L5, right) = 1.0$. This comes entirely from the immediate reward from L6.

And moving left from L5, $Q(L5, left)$:

$$
\begin{align}
Q(L5, left) & \leftarrow \underset{a'} {max} \left ( R(s') + \gamma \cdot Q(s', a') \right ) \\
V(s) & \leftarrow 0 + 0.9 \cdot 0.0 \\
V(s) & \leftarrow 0 \\
\end{align}
$$

There is no immediate reward from L4. From L4, the maximum Q-value out of it is currently 0 because we've not done enough journey's to raise it.

So for now, $Q(L5, left) = 0$,

If we were to consider $Q(L4, right)$ it would't have a zero value because to the right, there are non-zero Q-values out of L5. In this way, L4 gains Q-values.

This illustrates why it is important to run many journeys to improve the estimates of Q-values.

Maze Example With Python

Writing code to demonstrate reinforcement learning really helps us understand it. Let's start with a very simple 1-dimensional maze, just like the one we thought about above.

Let's start by importing useful libraries:

import numpy
import pandas
import random

We create a table of Q-values, initialised to zero. It's two dimensional because one dimension represents the state (position) and the other the action (left, right).

# Q state-action table, initialised with zeros
Q = pandas.DataFrame(numpy.zeros((2,6)), index=[-1, 1])

# print initial Q (state, action) table
Q

This creates a 2 by 6 table, with the horizontal rows labelled -1 and 1, for the left and right actions. The columns are the positions 0-5 in the very simple maze.

Printing the table, makes this structure clear.

To estimate Q, our agent moves around the environment. For simplicity, we can use a random walk, that is, move left and right randomly. Using the terminology, this is called a stochastic policy.

Let's write the code that does this random walk, before we dive into updating the Q values.

# run several iterations to iteratively estimate Q-values

# number of iterations (actions)
iterations = 20

# initial position
xpos = 3

for i in range(iterations):
    print("xpos = ",xpos)
    
    # set new position position according to random walk policy
    xpos_new = xpos + random.choice([-1, 1])
    
    # check new position doesn't fall outside maze bounds
    xpos_new = numpy.clip(xpos_new, 0, 5)
    
    # also check it doesn't hit target location
    if xpos_new in [5]:
        xpos_new = xpos
        pass
    
    # update position
    xpos = xpos_new
    
    pass

We've set the number of moves to 20, and the initial agent position to be 3, but it could have been any valid position.

You can see we that for every iteration, we create a new position which is randomly to the left or right of the current position. We then test this new position to ensure it remains within the bounds of the maze. In fact, the code simply clips position values to remain within the range 0 to 5.

We also check the new position ins't the target location 5 as we don't want to move into it.

Finally we update the position with this new position.

Printing out the position values confirm the agent moves according to a random walk in the maze, and doesn't fall outside or hit the target cell.

Great - the agent is moving around the maze.

Now we just need to use each position it lands on to estimate the Q values for actions from that position.

The following code is inside the loop, before the position of the agent is updated.

# consider all actions
for action in [-1,1]:
    xpos2 = xpos+action
    # if xpos2 is outside maze, continue
    if ((xpos2 < 0) or (xpos2 > 5)):
    continue
    
    # reward is at position 5
    reward = 0
    if (xpos2 == 5):
        reward = 1
        pass
        
    # max Q from next state
    maxQ2 = max(Q[xpos2])
    
    # update Q-table
    Q.loc[action,xpos] = reward + 0.9 * maxQ2
        
    pass

From the current position xpos, we look at the positions to the left and right xpos2. If the position xpos2 being considered is outside the maze, then skip the rest of the code and and look at the other direction if we haven't, and if we have, try another move.

We set a default reward to 0, and only change it to one if the position being looked at is the target at location 5.

Remember the update rule for Q-values is the immediate reward and the maximum of the Q-values of the actions out of the position being considered. This is easy to code in Python. Q[xpos2] gives us a column of both Q-values from xpos2, and calling max() around thus gives us the maximum of those values.

We finally set the current location's Q value to the reward added to the discounted maxQ2. You can see the discount is 0.9.

Let's see what the Q-value table looks like after a few iterations:

xpos =  3
      0    1    2    3    4    5
-1  0.0  0.0  0.0  0.0  0.0  0.0
 1  0.0  0.0  0.0  0.0  0.0  0.0

xpos =  4
      0    1    2    3    4    5
-1  0.0  0.0  0.0  0.0  0.0  0.0
 1  0.0  0.0  0.0  0.0  1.0  0.0

xpos =  4
      0    1    2    3    4    5
-1  0.0  0.0  0.0  0.0  0.0  0.0
 1  0.0  0.0  0.0  0.0  1.0  0.0


...


xpos =  1
         0        1     2    3    4    5
-1  0.0000  0.59049  0.00  0.0  0.0  0.0
 1  0.6561  0.72900  0.81  0.9  1.0  0.0

xpos =  2
         0        1       2    3    4    5
-1  0.0000  0.59049  0.6561  0.0  0.0  0.0
 1  0.6561  0.72900  0.8100  0.9  1.0  0.0

xpos =  3
         0        1       2      3    4    5
-1  0.0000  0.59049  0.6561  0.729  0.0  0.0
 1  0.6561  0.72900  0.8100  0.900  1.0  0.0

xpos =  4
         0        1       2      3     4    5
-1  0.0000  0.59049  0.6561  0.729  0.81  0.0
 1  0.6561  0.72900  0.8100  0.900  1.00  0.0

We can see that initially the table's values are mostly zero. After some iterations, the Q-values grow as a result of the random walk being next to the target location, and then being diffused along the maze using the discount.

Let's look at the Q-values table after 20 iterations.

There are some key features of this table:

• The Q-values get higher as we move to the right along the table. This makes sense as the target is on the right.
• At any location, actions to the right should have higher Q-values than to the left. We can see this by looking vertically along a column. The values along the bottom row are higher than the corresponding values along the top row.
• When in position 0, moving left isn't possible as that's the end of the maze. This is why the left action remains 0 here.

We can visualise the Q-values table.

# visualise the Q-value table

import seaborn as sns

sns.heatmap(Q, cmap='coolwarm', annot=True)

The resulting image is much easier to interpet.

The Python code for this simple example is online:

• https://github.com/algorithmicart/reinforcement_learning/blob/master/Reinforcement_Learning_1.ipynb

Extending the code to a 2-dimensional maze doesn't need any new RL ideas. We'll use the following 2-d map:

The robot starts at the top left and need to find the target goal at the bottom left. The maze itself has barriers, marked in red above.

The code itself is only slightly more complicated than the 1-d example as we now need to deal with four directions for the random walk. The Q-values table will have 4 rows for each of the 4 actions, right, down, left, up.

• https://github.com/algorithmicart/reinforcement_learning/blob/master/Reinforcement_Learning_2.ipynb

The following shows an example of the Q-values table after 1000 iterations.

Yours will might be different as the path chosen is random, but after many iterations, the numercial values should be converging.

We can see that the value of moving right from the starting cell is 0, because there is a barrier in the way!In fact the only valuable action is to move down.

You might be wondering how we encode 2-dimensional positions $(x,y)$ to states along the table? We simply map them like this $(x + 5 \cdot y)$.

Visualising the Q-values table meaningfully isn't easy unwell focus on one chosen direction. We can combine all the Q-values from a cell, that is, combining all the possible actions. If we chose the maximum instead of the sum or average, we get back the V "hotness" value we were thinking about right at the top of this article!

The python notebook shows how this visualisation is done. The result is interesting:

We can see that the hotness values direct the robot along the optimal path to the target. The heat map also shows a sub-optimal path which goes the long way around to the target.

Great!

Let's try an experiment to see what happens if we have an additional reward at the bottom right.

The resulting heat map looks like this:

We can see the two targets have paths that are of equal effort. When the robot reaches $(2,2)$ the choice to go right has an Q value equal to going doing. In a practical scenario the robot would choose randomly between two equal paths.

Let's move the second target to $(2,0)$ where we know it is harder to get to.

This is the resulting heat map:

We can see the optimal path is to the first target and not the longer journey to the second target. At the location $(2,2)$  the Q-value to the right is 3.8, and the value down is the higher 4.3

More Sophisticated RL

Ali gave us an insight into more sophisticated RL concepts that are necessary for more realistic problems.

In larger environments, it can be inefficient to spend lots of computation power exploring it with random or other walks. There can be a balance between an explore and exploit mode, where exploring is useful for finding new targets or better paths, and exploit takes advantage of known good paths.

In many real world scenarios, the environment isn't static. That means an action can lead to a different state when undertaken at a later time, because the environment has changed. Further more, the feedback to the learning agent can also change. This needs a probabilistic approach to learning where we think in terms of expected reward rather than a deterministic reward.

It can be useful to think a little more deeply about the relationship between an agent's policy and the Q-values that it learns. So far we've stuck with a random-walk policy, but we don't have to.

At a simple level, a bad policy will mean poor exploration of the environment, which may lead to a suboptimal solution, or non at all. In non-trivial examples, different policies will lead to different maps of Q being learned. This opens up a different area of policy learning where the aim is to learn which kinds of policy lead to optimal Q-value learning.

Ali also introduced a variant of RL called temporal difference learning, or TD learning,  which can be usefully applied to scenarios which don't have an obvious target state, and also scenarios with continuous rather than discrete states.

It may seem counterintuitive that we can learn before we reach a target state. The following quote referenced by the TD learning wikipedia page provides a good example of a continuous scenario where guesses about a reward can make sense:

"Suppose you wish to predict the weather for Saturday, and you have some model that predicts Saturday's weather, given the weather of each day in the week. In the standard case, you would wait until Saturday and then adjust all your models. However, when it is, for example, Friday, you should have a pretty good idea of what the weather would be on Saturday – and thus be able to change, say, Saturday's model before Saturday arrives."

Deep RL with Neural Networks

A key development in machine learning has been the combination of neural networks and reinforcement learning.

For larger and more complex scenarios, the number of states can be huge. Multiplied by the number of possible actions, the problem is even bigger.

With our simple 5x5 maze, there a 25 states, each with 4 actions, so we have 100 state-action pairs, if we avoid the fact that a small subset are not possible due to barriers. This is a small number for modern computing.

Ali presented similar numbers for chess and Go. Chess has 10¹¹¹ (1 with 111 zeros after it) state-action pairs, and go has a humongous 10³⁶⁰, which is larger than the number of atoms in the universe!

Neural networks provide a clever solution because they can take state and learn to approximate Q values in a way that is feasible, albeit approximate.

Instead of a very large Q-values table, we use a neural network which more compactly maps state and action to a Q-value. A common configuration is for a neural network to take state as input and output Q values for multiple actions.

What a neural network does that a table doesn't is discard less useful information, learning only those features and correlations which are actually useful to approximating the Q-values.

The downside is that the neural network output is even more of an approximation than the tabular approach, and can suffer the usual issues of non-global minima and even poor convergence.

Despite these issues, the advantage of making larger problems feasible are worth the effort of applying "tricks" such as experience replay to make the approach work.

And this is how achievements like an RL agent learning to play classic Atari games using the  raw screen bitmaps as input have happened.

DeepMind RL agent trained to play classic Atari games
https://deepmind.com/research/publications/playing-atari-deep-reinforcement-learning

Creative Applications

RL is primarily applied to industrial applications, because it is about an agent interactively in an environment which provides feedback towards a set of goals. This is why the robot analogy reflects RL concepts very well. Ali's example of Facebook using RL to decide on the timing of notifications to optimise user interaction also matches the RL framework very well.

In terms of generative design, Ali discussed how RL is employed in drug design.

As a contrast to industrial applications, Ali did present some creative applications. One that caught the audience's attention was teaching an agent to drive off-the-shelf graphics creation software to draw portraits.

The following shows faces being drawn by an agent trained using RL with a reward based on its ability to fool a discriminator in the context of a GAN architecture.

DeepMind SPIRAL: https://github.com/deepmind/spiral

Thoughts 

There was an hour of Q&A after Ali's talk which shows how much interest there is in the subject, and how well he inspired the group.

During the discussion Ali made a very interesting point that the latest neuroscience research suggests that the human brain makes many predictions before acting, and then uses feedback to reinforce its understanding of the world.

This underlines the importance of predict, trial, reward and update mechanism as a learning framework towards a potential general intelligence.

Another very interesting question was about the equivalence between genetic algorithms and reinforcement learning. This provoked a lot of thought and discussion after the meetup itself.

At one level, all machine learning is equivalent in that a model is updated based on observation. More useful are the higher level abstractions. Both GA and RL learn solutions to a problem, with fitness based on feedback from the environment. A key difference is that standard RL takes feedback more directly from an achieved goal or target, whereas GA takes feedback from a more continuous measure of success, fitness. A RL method is more amenable to exploring an unknown environment whereas a GAs require some domain or model knowledge.

And this is the key advantage of RL - very little domain or model knowledge is required.

A very important point that emerged after the talk is the comparison between the energy efficiency of RL algorithms and that of the human brain. The human brain appears to do far more with very little energy consumption compared to the energy needs of modern machine learning methods including RL.

More Reading

• Dictionary of RL terminology: https://towardsdatascience.com/the-complete-reinforcement-learning-dictionary-e16230b7d24e
• An excellent book on machine learning, with one of the clearest explanation of RL in chapter 13 (pdf): http://profsite.um.ac.ir/~monsefi/machine-learning/pdf/Machine-Learning-Tom-Mitchell.pdf
• UCL RL Course Slides: http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html
• History of RL by Prof AG Barto: https://www.youtube.com/watch?v=ul6B2oFPNDM
• MIT Intro Lecture on RL video: https://www.youtube.com/watch?v=zR11FLZ-O9M
• Google Depmind's AlphaGo Zero beats world-leading human Go player: https://deepmind.com/blog/article/alphago-zero-starting-scratch, https://www.nature.com/articles/550336a.epdf
• SPIRAL for painting faces: https://github.com/deepmind/spiral
• Good overview of RL: https://neuro.cs.ut.ee/demystifying-deep-reinforcement-learning/