Algorithmic Art: Introduction To Creative Coding With Recursion

This month we held the second Cornwall meetup, following on from the first one which started introducing creative coding with p5js.

This time we continued our learning to code and focussed on recursion - a powerful concept that can elegantly create intricate patterns, but one which some people find difficult to get started with.

The slides are here: [link].

Because we've covered recursion before in London, this post will focus on the keys points and improvements over the previous session.

Examples Of Recursive Patterns

We started by looking at a few examples of patterns and discussed the common thread between them - that of self-similarity.

We looked at geometric patterns as well as natural forms, such as this fern leaf.

We briefly touched on the idea that self-similarity at different scales is one design strategy for beauty, and nature is a bounty of such fractals.

Pure mathematics itself, far from being predictable and boring, has within it's structures beautiful organic self-similar forms, such as this Julia set.

We also noted the use of self-similarity in art, with the Droste example from 1904, and another example of Christian art going back to about 1320.

An Apparently Unhelpful Conversation

We then discussed a conversation happening amongst Victorian ladies in the evocative setting of a rose garden.

The first lady is asking "what is 3", to which the reply is "1 more than 2". The first lady then asks "what is 2", to which the reply is "1 more than 1". Again, the first lady asks "what is 1" to which there is finally a concrete answer.

The second lady looks like she's being particularly unhelpful but she's actually being rather clever. She is using only two phrases:

"1 more than .."
"that's how many noses you have"

With just these two definitions she is able to reply to any question from the first lady about any number.

Although this is a contrived example, the key point is that a small number of definitions can describe many more things - a concept key to using recursion.

Coding A Self-Similar Pattern

We then looked a simple, but still self-similar pattern, and asked ourselves how we could write code to draw it.

We noticed that the main pattern has two smaller versions of itself to the left and to the right.

And that means each of those has an even smaller version attached.

This description of the pattern is recursive - it is defined in terms of itself.

We then started to think about how to code, not an easy task when trying it for the first time. We started by taking small steps, and coding the big central circle.

That's easy enough but only draws a single yellow circle. Now we need more code to draw the other circles. There are lots of them .. does that suggest lots of circle() code instructions?

That goes against the key idea of using a small number of rules to describe something more complex.

Instead, let's try to write code which expressed the idea that the main pattern is a circle with two smaller versions of the same pattern.

This looks like it shouldn't work. How can we describe something in terms of itself. Surely we haven't really defined it? Isn't this a logical error?

Turns out that many programming languages do allow you to create such definitions - recursive definitions.

Mind blowing!

Make Sure To Stop!

Before running the code, I told the group there was one important problem with the code, and asked them to see if they could spot it.

The code as we wrote it would never stop. The my_pattern function would call my_pattern, albeit with a smaller size, which would call my_pattern ... and so on .. until the code crashed.

We need to establish a limit to how deep the recursion goes. There are many ways to do this, and a simple one is to stop when the size gets smaller than a threshold.

Finally we had code ready to run.

The result so far is a series of circles getting smaller to the right. That's because our code only defines the pattern as having a smaller version of itself to the right. We need to add the left side too.

And finally we have the pattern we wanted.

The striking thing here is how a small change to the definition results in a drastic change in teh pattern.

We look at other examples of patterns which were based on the very same simple code but with small variations. This next one defined a pattern as having smaller versions of itself not just to the left and right, but above and below too.

The code for this pattern is online and worth exploring:

https://www.openprocessing.org/sketch/642059

A Framework for Recursion

We looked again at the code for the pattern made of circles and noted some key elements.

The code has a termination rule, a rule that decides when to stop going deeper into the recursion. There is also code which defines what the detail is at the current level of recursion. Finally there is a continuation rule which defines where the next next level of detail is.

This is a general framework that is useful to planning your own code, or seeing if a problem can be solved elegantly in a recursive manner.

Randomness and Recursion

There is no reason we can't combine different ideas with recursion, randomness for example.

We looked at a pattern where the next level of detail could be one of two options, chosen at random when drawn.

You can see the main pattern is composed of squares, but the next level of detail has squares either top-left to bottom-right, or top-right to bottom-left.

The results are different every time the code is run.

You can explore the simple code yourself ere:

https://www.openprocessing.org/sketch/658450

Natural Forms

We then discussed recursive natural forms, taking inspiration from nature itself. We looked at a tree in winter, when its branches are more visible. We noticed that roughly speaking, a tree is made of smaller trees emerging from a branch - a recursive pattern.

We don't have to encode all the details of a real tree, often a simplification is interesting by itself. Here is the simple idea of a tree being defined a s branch with two smaller trees emerging form the end of it.

And of course each of those smaller trees will have a branch with even smaller trees.

We can encode these ideas using the framework we discussed earlier.

And the results are really rather effective! This rendering does make two further refinements, it reduces the thickness of the branches deeper into the recursion, and also varies the green hue randomly too.

You can explore the surprisingly simple code here:

https://www.openprocessing.org/sketch/642756

The code does use trigonometry because it deals with angles and directions for emerging branches. The maths for this is not that difficult, but too many people have a negative feeling about it from a poor experience at school.

I was really pleased that an artist in the group did want to explore trigonometry and we worked through a simple example at the end of the session.

We finished that section by looking at a bubbly recursive pattern developed by a member of the group from the session in London, and discussed how angles and trigonometry were used to place three bubbles on the edge of a bubble, and then smaller ones on those, and so on...

You can explore the code yourself at:

https://www.openprocessing.org/sketch/658493

Gallery

We took some time to have a go at developing recursive patterns ourselves. Here are some examples.

You can find links to these designs in the meetup comments. It is interesting how different ideas result in quite unique patterns.

Growing Code

As a bonus we looked briefly at using recursion not to grow a pattern, but to grow code that itself draws a pattern!

We'll look at this idea properly at a future session, but this taster showed that there are no limits to how creative we can be in combining algorithmic ideas, not just combining colours and shapes.

We looked at turtle code (L=left, R=right, F=forward, etc) which can be used to draw patterns. Some examples are show here. You can see how FRFRFRF draws a square.

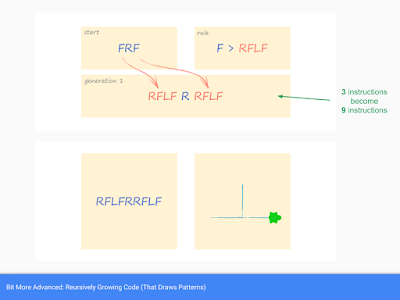
We can use a recursive rule to relate the next generation of the code to a previous one through a simple growth rule. The next picture shows how turtle code FRF is turned into RFLFRRFLF using the rule F>RFLF which mean grow every F into RFLF.

The 3 instructions of FRF are grown into 9 instructions. The pattern drawn is an upside down T.

Growing the code to the next third generation creates 21 instructions, and an interesting looped pattern.