This
month we had a gentle introduction to
recursion - a powerful idea that can create wonderful patterns - but one that we sometimes struggle with when we first come across it.
Here's an example of the kind of pattern that can emerge from recursion.
The
slides are always at:
[link]. The slides also contain links to
code you can experiment with.
Aim
The aim of the session was try to:
- explain what recursion is, and to be able to recognise it when others use it
- use simple examples to get a feel for the mechanics of recursion
- to develop a way of thinking which can help make our own recursive algorithms
And to inspire members to try their own ideas for recursive algorithms.
Start With Observation
We warmed up by looking at a few examples of patterns and natural forms. We observed that a common theme amongst the images was self-similarity at different scales - which some knew to call
fractal.
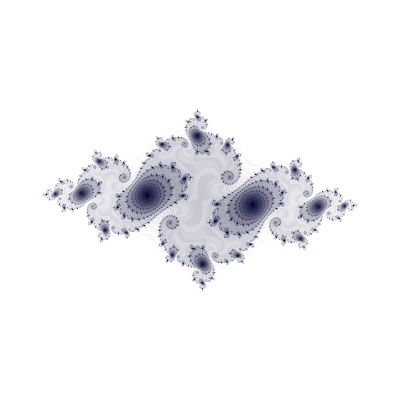
A good example was from nature itself - a fern leaf. Looking at the fern above, we can imagine snipping off one of the branches, and examining it to find that it looks remarkably like the whole. In fact the snippet itself has smaller branches. When you're looking for self-similarity, you start to see it everywhere - from the artery structure of a human body to the fluffy clouds in a summer sky, from the lumps and bumps of a mountain, to the repeated motif of purely mathematical fractals like this
Julia fractal.
After a few examples, our mind's eye was primed to spot this kind of self-similarity for the rest of the talk.
An Apparently Unhelpful Definition
We started our discussion, not by defining recursion or talking about someone else's definition. The reason many of us were here is because that approach hadn't worked!
We started instead by pondering this interesting conversations between ladies in a Victorian garden:
We overhear a lady asking another lady (with the rose), "what's 3?". The reply is "1 more than 2". That doesn't seem very helpful, so the lady asks again, "what's 2?". Again the reply is "1 more than 1". How annoying! The lady tries again, "what's 1?". This time the reply is a little bit more helpful, "that's how many noses you have."
It does seem like the lady with the rose is being very obtuse and determined to be unhelpful. I'm not sure I'd enjoy a conversation like that. Imagine if I'd started with "what's 100?" - the conversation would have been very long and boring.
Let's look at the conversation from a different perspective.
The lady with the rose has actually been very clever. She has only used 2 kinds of responses:
- "1 more than ...."
- "that's how many noses you have".
Using only these two responses, she is able to describe any whole number, be that
3,
7,
99 or even
22139. Sure, the conversation that starts with
"what's 22139?" will be long and boring, but remember that we can offload repetitive and boring tasks to our computers to do quickly and without fuss or boredom error.
Let's say that again - the lady with the rose, has been able to describe any one of the infinitely many whole positive numbers using just those 2 rules. That's pretty amazing!
Visual Patterns with Just Two Rules?
Then came a thought leap. What if .. what if it was possible to describe complex patterns using just 2 rules?
That's a powerful and ambitious statement. But let's start with a not so complicated pattern so we can focus on the idea first.
Here are the ladies describing circles.
Again, the lady with the rose is able to respond to questions about circles of any size using only 2 replies:
- "... one size bigger than ..."
- "O"
And again, her approach is clever, because with just those 2 rules, albeit with lots of repetition, she is is able to describe circles of any size.
We then tried to visualise this mechanism of describing something in term so the next thing, whether that's a number or a circle. Visualising something, or even trying to visualising something, is a good way of developing empathy with the mechanism at play.
We did this visualisation with just "pen and paper" not with code, to keep our focus on what's important - the concept. We started with the idea of a circle of size 3, which is one size bigger than a circle of size 2 .. which is one size bigger than a circle of size 1 .. and a circle of size one is just O. This resulted in a picture of concentric circles with the largest being of size 3.
We then asked ourselves the question - what if we had started at size 4? We know a circle of size 4 is one size bigger than a circle of size 3. That means the picture we drew starting at size 3 can be reused. We've already done the work for circles of size 3, 2 and 1. The overall picture is a little bit more complex than the one starting at size 3.
Although these concentric circles aren't very intricate in design, we can start to see how the very same 2 rules can be used to create more and more complex or detailed patterns.
Coding
We then started thinking about how we might write code to create the previous pattern, which is visualising the relationship between circles of different sizes, as defined by the 2 rules.
To keep things clear, we wrote in plain-English pseudocode, avoiding the distractions of real programming languages and their peculiar syntax.
Our first attempt was to simple three instructions to draw a circle: circle(size = 3), circle(size = 2), and circle(size = 1). That would certainly create that pattern of three concentric circles.
But - what if we wanted to start with a circle of size 100? We'd have to write out 100 different circle() commands!
We'd forgotten the clever ladies in the Victorian garden. They were clever enough to be able to describe numbers or circles of any size with just 2 rules. They didn't need 100 statements to describe 100 different circles.
We tried again, this time trying to reflect the ladies' approach:
Here we're saying "let's draw a pattern of size 3", and we're defining that pattern.
The definition of a pattern of size s is a circle of size s, and a smaller pattern of size s-1. That needed a bit of thinking but is it does reflect the ladies' thinking - defining one thing in terms of the next thing.
It can seem strange that we are allowed to define something in terms of itself, especially in a computer programming language - but many programming languages do allows us to do this - and it is incredibly useful.
And definitions which refer to themselves are recursive definitions - hence the word recursion.
Logic Error!
Let's see what happens if we invoke that newly defined my_pattern() with an size of 4, that is, my_pattern(4).
We expect to see a pattern of 4 concentric circles, like this:
If we actually ran that code, it's unlikely that we'd see these 4 circles.
Instead we'd probably find our computer giving us an error, or becoming unresponsive. Why?
If we look again at the code, and follow it through step by step, we can see what happens:
- my_pattern(4) means a circle of size 4, and then my_pattern(3)
- my_pattern(3) means a circle of size 3, and then my_pattern(2)
- my_pattern(2) means a circle of size 2, and then my_pattern(1)
- my_pattern(1) means a circle of size 1, and then my_pattern(0)
- my_pattern(0) means a circle of size 0, and then my_pattern(-1)
- my_pattern(-1) means a circle of size -1, and then my_pattern(-2)
- my_pattern(-2) means a circle of size -2, and then my_pattern(-3)
- .... and so on
Our code doesn't stop at circle size 1 ... it carries on.
We missed one of the two rules that the ladies' discussed, the rule that terminates this chain. With the numbers example, the rules terminated at number 1, and the circles example terminates at circle size 1. We need to terminate this pattern at pattern size 1.
Let's try again, and this time care care to include both rules:
Here we've written code to explicitly reflect the 2 rules - which we've called the continuation rule, and the termination rule. One rule checks to see if the termination condition has been reached - pattern size 1 - and if it has, then we draw the circle size 1 and finish. If we haven't reached the termination condition, we draw the circle of size s, and continue with a smaller pattern of size s-1.
Recursion - Termination and Continuation Rules
We talked about the generality of this approach in all recursive definitions:
- a continuation rule - which defines how the current level of detail relates to the next level of detail
- a termination rule - with defines when the continuation stops
Continuation links one level of detail to the next level of detail. It's the clever bit which recognises a symmetry or pattern that we can use to link, and keep linking, one level of detail or size to the next.
Termination is critical - without it the continuation never stops. That might be fine in pure mathematics (eg 1 + 1/2 + 1/4 + 1/8 + 1/16 ... = 2) but when computing we can't continue to infinity.
We talked about trying to think of imagined patterns, or even forms that we see in nature, in terms of these 2 rules - good practice for becoming a more proficient algorithmic artist.
Hard Work Pays Off
Once we've put the effort into defining a pattern recursively, using the two rules, we can start to reap the benefits.
What happens if we invoke my_pattern(10). We automatically get a pattern of 10 circles! No additional work needed to be done by us.
That's an important point. Once we've invested the effort think recursively, and define the pattern recursively, we can then very easily draw patterns of many sizes, or levels of detail.
This goes right back to the original chat the ladies had, where the lady with the rose cleverly defined rules which could describe any positive whole number.
We could easily invoke my_pattern(1000) if we wanted to, and we'd get 1000 concentric circles.
More Interesting Patterns
Once we've got used to the the key idea of recursion and recursive thinking, we can then have a lot of fun experimenting and extending the ideas.
We discussed an imaginary pattern called The Mysterious Holocrux, which the ladies defined as a circle with two smaller holocrux patterns either side of it.
Here's a sketch of what a holocrux of size 300 looks like - a circle of size 300, with a holocrux of size 200 either side of it.
We can fill in the blanks - because the same rules tell us what a holocrux of size 200 is.
If we carry on to the next level of detail ...
This is just like the concentric circles example but the next level of detail has 2 circles for every 1 circle, and they're shifted along rather than remaining centred on the same point.
When we talked about coding this idea, we introduced a new idea.
We've combined the termination and continuation rules. The logic is still the same, but the programming language allows us to express both concisely. Here, when we say "continue as long as the size s is more than 0" we're expressing both rules:
- termination when the size is 0 or less
- continuation as long as the size is more than 0
This is actually a very common way of coding recursive algorithms so worth getting used to spotting.
The results are starting to look more interesting than concentric circles.
That pattern could do with more details, so let's change the logic so that the recursion continues for longer as the circles get smaller. Let's also change the rate at which circles get smaller.
We introduced a new idea again. This time the termination condition was changed to s > 5, and not left as s > 0. We discussed why this might be.
The reason is that we're halving the size of the circles with every continuation. No matter how many times we halve a number, we never get to zero. That would mean our computers groan, become unresponsible and throw us an error. That's why we need to stop when size reaches a number bigger than 0, like 5.
Here's the result.
That's much more interesting than anything we've seen yet. And we're starting to see the power of recursion and the intricate patterns that might be possible.
We then saw how easy it was to extend an existing recursive pattern. The holocrux was defined a extending horizontally with every continuation. We can add a vertical extension too.
Now, a holocrux of size s, is a circle of size s, with 4 smaller holocrux patterns above, below, to the left and to the right of it.
The code changes are minimal - a benefit of the investment we made earlier.
And the result is really rather interesting.
The ease of extending a core recursive pattern was stressed again - it's a benefit of putting the effort in early on to cast imagined patterns in terms of a termination and continuation rule.
Its super-easy to take that last pattern, and tweak how far out the smaller holocrux patterns are placed. We can even change the colouring scheme - here we're using a translucent red for the circles.
Playing and experimenting is definitely encouraged.
Randomness and Recursion
Randomness is a powerful algorithmic art method in its own right. Could we usefully combine it with recursion?
We talked about another imagined pattern the Jewel of Drax. It's very similar to the holocrux, but is based on squares not circles. The important difference is that the next level of detail could be one of two options.
When we continue the recursion and define the next level of detail, we choose one of two possible options, chosen with equal probability:
- 50% chance - jewels of drax placed top right and bottom left
- 50% chance - jewels of drax placed top left and bottom right
We've introduced an element of chance into the recursive pattern - with means the results will be different every time we run our code. Here are the results from four runs.
Randomness adds a particularly unique dimension to recursive patterns.
We continued to explore a slightly more involved example, inspired by nature - a tree in Richmond park in fact!
We can see that the tree is self-similar in it's branching. A chosen branch could be the whole tree, or a snippet form a larger branch.
We can formulate a recursive pattern for a tree:
- continue: a tree of depth 3 is a branch with two trees of depth 2 emerging from the end of the branch
- terminate: a tree of depth 1 is just a branch
A picture explains the idea better:
The initial results weren't very natural.
The branching is there and works fine but the overall structure is too regular. Let's introduce some randomness to the direction of the emerging branches. Here are the results of four runs.
Much more interesting and sometimes rather pleasing too. We can refine the trees further by making the branches thicker for larger depths, which results in thinner outer branches. We can also link the length of the branches to the depth, so that branches get shorter further up the tree. The results are more grasslike and really rather nice!
Nice!
Quick Test
As a test of our abilities to spot recursion we looked at these bubble images.
After some observation it because clear that the patterns are random but start with a circle with has 3 smaller circles placed at a random location on it's edge .. and those circle too have their own circles.. and so on.
This pattern was inspired by the work of an Algorithmic Art member who created a similar work at a previous hackathon.
Summary
The key points to take away were repeated - trying to think about patterns in terms of a continuation rule and a termination rule. These might be patterns we see in nature, or patterns we're imagining.
Hopefully, the session clarified recursion, and more importantly, showed it working. A few members were inspired to try their own recursive pattern ideas - which is great!
A Slightly More Advanced Idea
At the end of the session we briefly talked about a slightly more advanced idea.
Instead of us writing code which draws patterns .. why don't we write code which grows code recursively ... and see what patterns that makes?
This is interesting on several levels. The idea of code writing code is interesting in itself. The idea of growing code recursively is really interesting too.
We started by defining a simple "turtle code' language with commands like L for left, F for forward, R for right. We also included commands to save and restore state, [ and ]. We saw how even this simple language could draw a very wide variety of patterns - the simple turtle code language is very expressive.
We then grew the code according to simple replacement rules. Each application takes a generation of code to create the next generation of code.
Here we see the extremely simple starting code FRF have the rule F > RFLF rule applies to grow the first generation of code RFLFRRFLF and then again to grow the second generation of code which has 21 instructions.
The size of the code grows rapidly. Generation 16 has 393,213 instructions - that's over 1/3 of a million!
The resulting pattern is intricate and self-similar. Although this particular one doesn't look very pleasing, close up it is more interesting.
This method of growing code produces a wide variety of patterns .. including trees!
Other patterns that a little experimentation found include beehives, geometric growths, curly curls and rather ominous spikes.
Feedback
It's always useful to get feedback on the group's sessions. I was really pleased that many members do want more sessions aimed at beginners - they do seem popular.
Demand for more practical hands-on sessions is strong, so we'll do more in future.
Overall I was really pleased that some members were inspired to try these ideas themselves.